ADAS-Radar|一文入门汽车毫米波雷达基本原理
引言
刚接触毫米波雷达的时候并不清楚它是如何用2Tx天线加4Rx天线就能做到多目标检测,随着学习的不断深入,才恍然大悟,科学真的很奇妙!信号与系统老师诚不欺我!
随着现代社会对于安全驾驶和智能交通的不断追求,汽车技术正朝着前所未有的高度发展。其中,毫米波雷达技术作为一种先进的传感器技术,正在引领着汽车领域的革命性变革。毫米波雷达以其高精度、可靠性和适应性,在自动驾驶、碰撞预警、自适应巡航控制等关键领域发挥着不可或缺的作用,将汽车的安全性、便捷性和智能化水平推向新的高度。
1.Introduction
毫米波雷达作为一种主要的感知技术,在汽车安全系统中扮演着重要的角色。它利用毫米波频段的电磁波来感知周围环境,并通过测量反射回来的信号来检测和跟踪其他车辆、行人、障碍物以及道路状况。
与传统的红外传感器和激光雷达相比,毫米波雷达具有独特的优势。它能够利用毫米波频段的电磁波,穿透恶劣天气条件,如雨、雪和雾,从而实现在复杂环境下的可靠探测。
本文将重点介绍汽车毫米波雷达的原理和工作方式,我们将简要解释毫米波雷达的基本原理,包括其工作频段和探测原理。
2.FMCW雷达介绍
2.1 基本概念
目前市面上毫米波雷达基于连续波调频 (FMCW)技术,因此下面我们将以FMCW雷达指代毫米波雷达。顾名思义,FMCW 雷达连续发射调频信号,以测量距离以及角度和速度。FMCW雷达通过反射信号的相位以及频率来定位、测速、测速等,这与激光雷达周期性发射短脉冲然后通过直接测量返回时间的原理不同。(关于激光雷达原理可以看我公众号另外一篇文章 激光雷达基本原理详解)
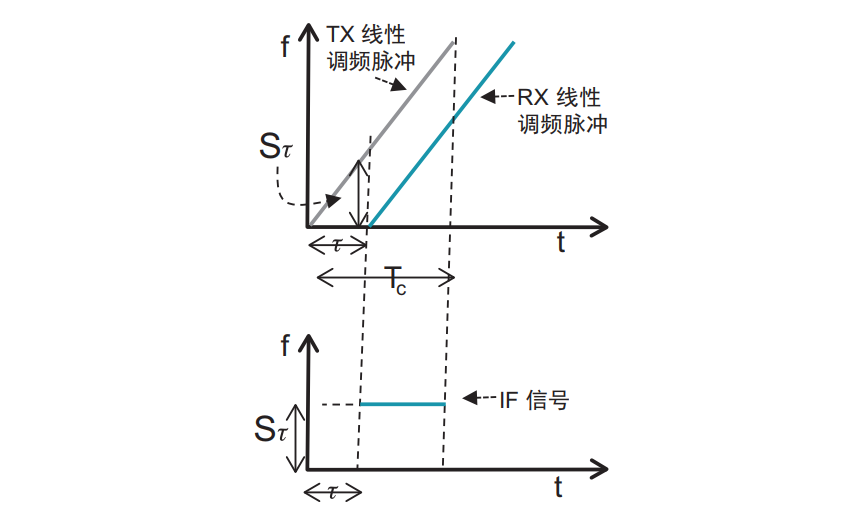
FMCW雷达系统所用信号的频率随时间变化呈线性升高。这种类型的信号也称为线性调频脉冲。 下图以幅度(振幅)相对时间的(A-t)函数,显示了线性调频脉冲信号表示。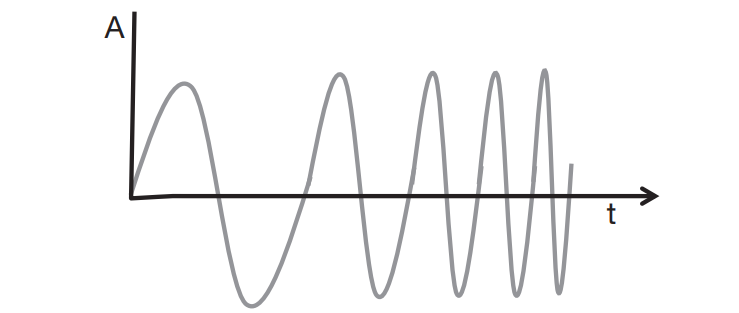
以纵轴为频率,横轴为时间,则其(f-t)图像表示如下所示: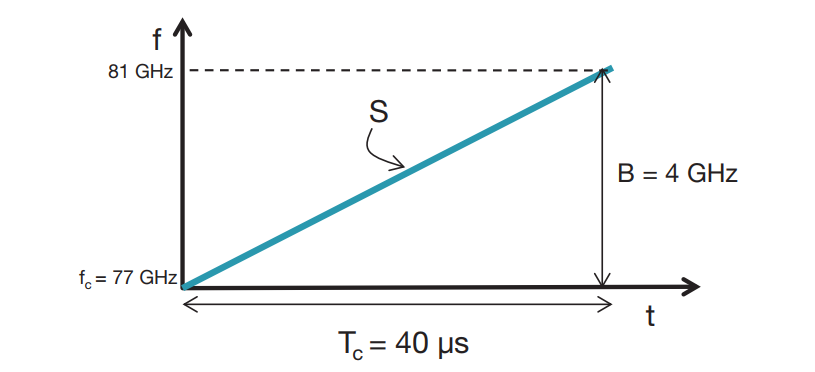
2.2 基本框架
FMCW雷达基本框架如下所示:
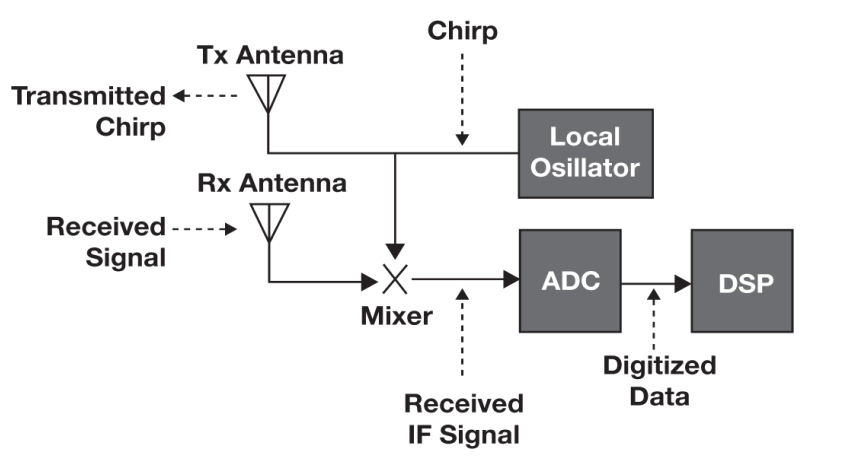
可以看出,FMCW雷达由下述基础组件构成:
- 发送天线(Tx Antenna)&接收天线(Rx Antenna)
- 混频器(Mixer)
- 时钟源(晶振)
- ADC & DSP
2.3 工作流程
雷达工作流程如下:
- 合成器生成一个线性调频脉冲;
- 该线性调频脉冲由发射天线(TX 天线)发射;
- 物体对该线性调频脉冲的反射生成一个由接收天线(RX 天线)捕捉的反射线性调频脉冲;
- “混频器”将 RX 和 TX 信号合并到一起,生成一个中频 (IF) 信号。
其中:
混频器是一个电子组件,将两个信号合并到一起生成一个具有新频率的新信号。
其解释如下:
对于两个正弦函数信号$x_1$和$x_2$如下:
$$
x1=sin(w_1t + φ_1) \
x2=sin(w_2t + φ_2)
$$
对于输出$x_{out}$有一个瞬时频率,等于两个输入正弦函数的瞬时频率之差。输出$x_{out}$的相位等于两个输入信号的相位之差,如下:
$$
x_{out}=sin((w_1 - w_2)t + (φ_1 - φ_2))
$$
3.测距原理
3.1 雷达信号
以单个物体检测为例,使用时间对频率(f-t)图像对于 Tx、Rx 以及混频的 IF 信号的表示如下所示:
可以看出混频信号IF是一个频率固定的正弦信号$Asin(2πf_ot+φ_0)$。
3.2 距离计算
假设物体的距离为$d$,那么 Rx 与 Tx 之间的延时 $τ$ 计算如下:
$$
τ = 2d / c
$$
其中:$d$ 是距离,$c$ 是光速
注意: $d$ 是待测目标距离,而$τ$是电磁波的飞行时间,由于飞行时间极短,因此如果直接对$τ$使用硬件测量成本极高(参考激光雷达)。
所以: 这里换一个方式,我们通过FFT反推信号的频率和相位,转换得到速度、距离等信息,推导过程如下:
高中三角函数学过,旋转角频率$w$和频率$f$之间关系如下:
$$
w = 2πf
$$
那么对于 Rx 以及 Tx 混合得到 IF 信号的初始相位有:
$$
φ_0 = w_c * τ = 2πf_c τ
$$
其中:$f_c$是雷达的Tx信号的初始频率
由于:
$$
τ = 2d / c
$$
因此:
$$
φ_0 = 2πf_c2d / c = 4πf_cd / c \
= 4πd/λ
$$
其中,$λ$为初始信号波长($c=f_cλ$)
其次,根据FMCW测距原理图像,可知混频 IF 信号其频率$f_o$为
$$
f_o = 2Sd/c
$$
其中:$S$为FMCW频率变化率,单位为Mhz/s
那么,IF 信号可以表示如下:
$$
IF = Asin(2πf_ot+φ_0)
$$
其中:$f_o = 2Sd/c$,$φ_0 = 4πd / λ$
到这里,我们便可以知道,对于一个反射物体,我们对 IF 信号做FFT,可以知道其频率$f$以及相位$φ$,那么其距离为:
$$
d = f_oc / 2S = φ_0c/4πf_c
$$
一般计算时我们选择频率计算即可。
3.3 多目标距离计算
对于多目标物体,IF混频信号则由多反射目标距离不同,那么反射回来图像则如下所示:
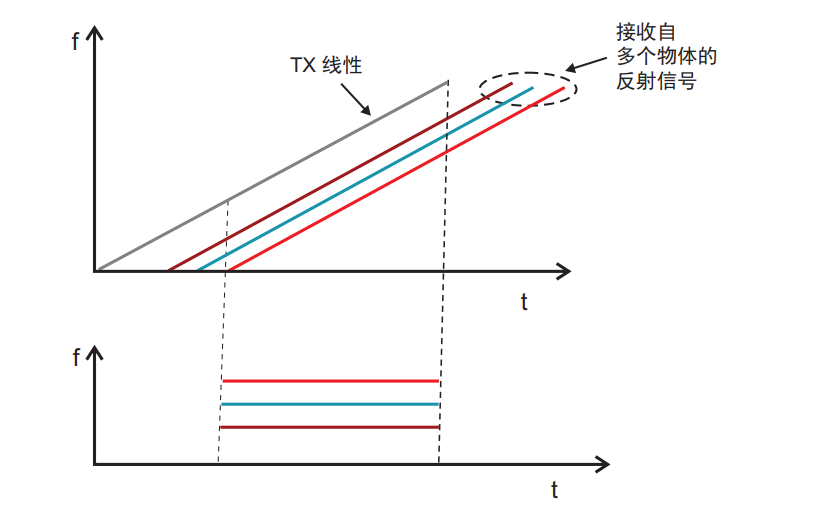
可以看出,多目标反射则对应多个Rx信号,其频率与相位均不相同。对IF信号做完FFT之后可以得到多个主干频率如下:
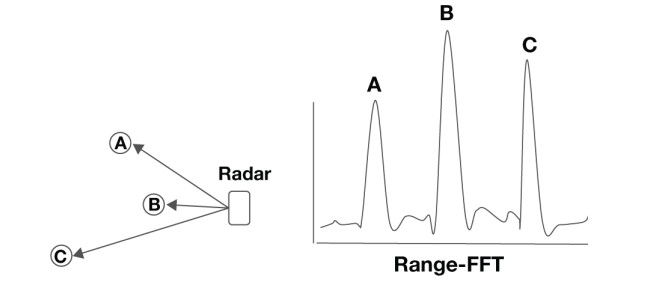
通过$d = f_oc / 2S$ 则可以分别计算出这三个物体的距离了。
3.4 距离分辨率计算
距离分辨率是辨别两个或更多物体的能力。当两个物体靠近到某个位置时,雷达系统将不再能够将二者区分开物体。傅里叶变换理论指出,通过延长 IF信号,可以提高分辨率。
但要延长 IF 信号,还必须按比例增加带宽。延长的IF 信号会产生一个有两个分离峰值的 IF 谱。
傅里叶变换理论还指出,观测窗口 (T) 可以分辨间隔超过 1/THz 的频率分量。这意味着只要频率差满足下面公式中给出的关系,就可以分辨两个 IF 单音信号。
$$
Δf>1/T_c
$$
其中$T_c$是观测时间长度,即做FFT信号时间长度。
而由于:
$$
Δf=2SΔd/c
$$
则有
$$
Δd>c/2ST_c=c/2B (B=ST_c)
$$
因此距离分辨率有:
$$
Δd_{res}=c/2B
$$
因此,对于带宽为 Ghz 的FMCW雷达,大概为cm级别的分辨率,例如带宽$B=4Ghz$线性调频脉冲带宽的的雷达距离分辨率为3.75cm:
$$
Δd_{res}=c/2B=0.0375m
$$
好了到这里距离已经计算出来了,那么速度、角度是怎么计算出来的呢?请继续往下看!!!
4.测速原理
4.1 Radar测速信号
为了测量速度, FMCW 雷达会发射两个间隔 $T_c$ 的线性调频脉冲。每个反射的线性调频脉冲通过 FFT加以处理,以便检测物体的距离,这个FFT称之为距离FFT。对应于每个线性调频脉冲的距离 FFT 将在同一位置出现峰值,但相位不同。该测得的相位差对应于速度为 $vT_c$ 的物体的移动
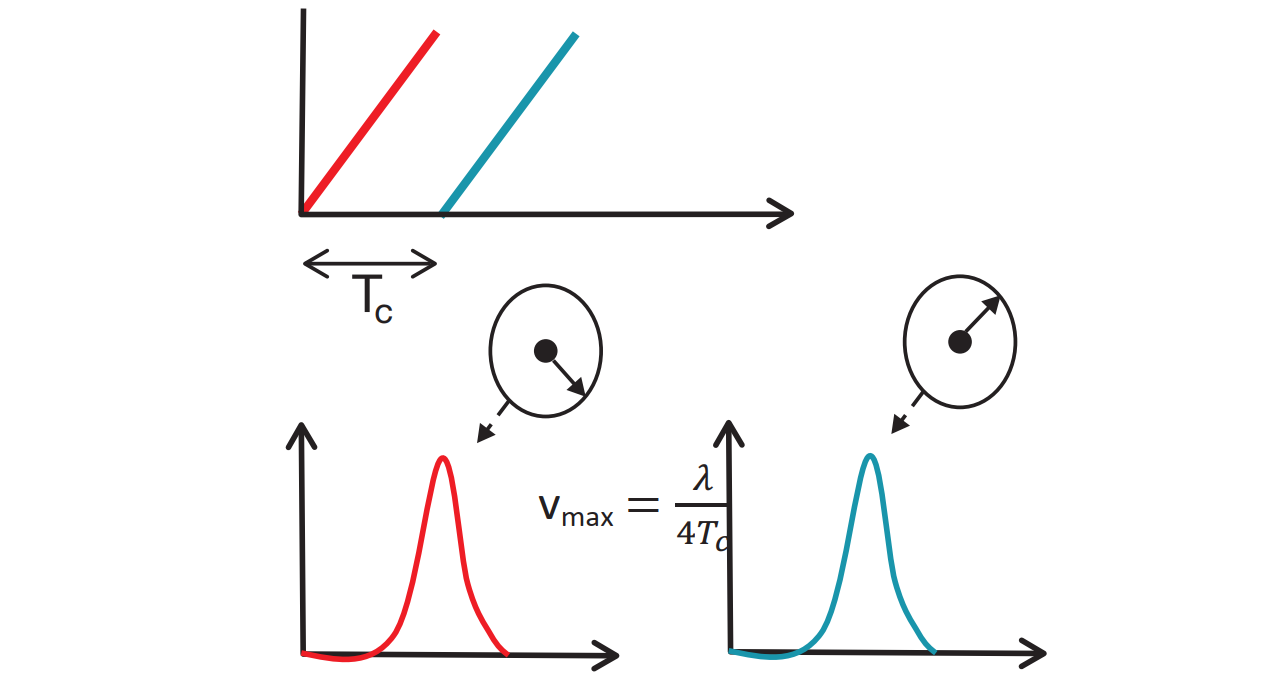
通过相位差公式$φ_0 = 4πd / λ$我们可以知:
$$
Δφ=4πΔd/λ=4πvT_c/λ
$$
则有:
$$
v=Δφλ/4πT_c
$$
由于速度测量基于相位差,因为相位存在周期性为$(-π,π)$,因此会存在模糊性或者周期性。这种测量仅在 $|Δφ| < π$ 时具有非模糊性。
故可知 当$|Δφ|= π$,雷达最大可测量的速度为:
$$
v_{max}=λ/4T_c
$$
4.2 同一位置不同物体速度测算
如果速度不同的多个移动物体在测量时与雷达的距离相同,则双线性调频脉冲速度测量方法不起作用。这些物体由于与雷达的距离相同,因而会生成IF 频率完全相同的反射线性调频脉冲。因此,距离FFT 会产生单个峰值,该峰值表示来自所有这些距离相同的物体的合并信号。简单的相位比较技术将不起作用。
在这种情况下,为了测量速度,雷达系统必须发射两个以上的线性调频脉冲。它发射一组 N 个等间隔线性调频脉冲。这组线性调频脉冲称为线性调频脉冲帧。
下图显示了一个线性调频脉冲帧随时间变化的频率:
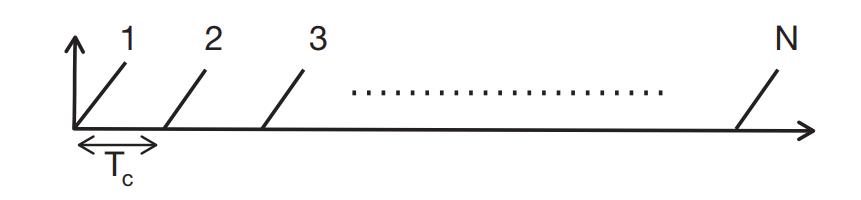
距离 FFT 处理反射的一组线性调频脉冲,从而产生一组 N 个位置完全相同的峰值,但每个峰值都有一个不同的相位,包含来自这两个物体的相位成分(来自各个物体的单独相位成分由下图中的红色和蓝色相量表示)。

这个里 $v_1$ 和 $v_2$ 通过多普勒FFT则可以获取,即对n组信号的每个信号单独做FFT,具体可以参考下图:
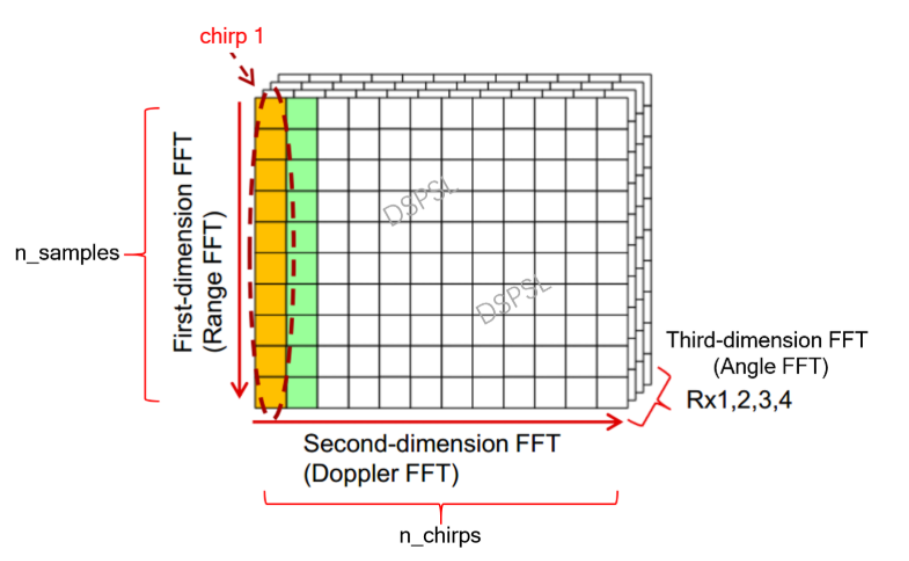
通过多普勒FFT,便可以区分出两个不同速度物体:
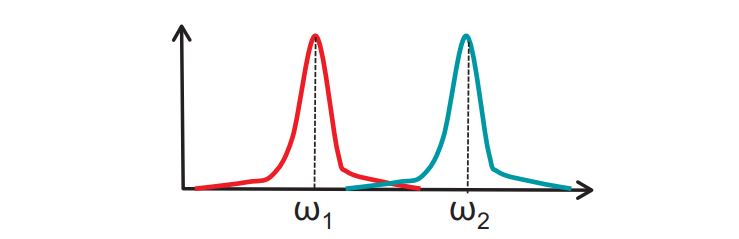
其中 $w_1$ 和 $w_2$ 对应于各个物体连续线性调频脉冲之间的相位差,则两个物体的速度可以得到如下:
$$
v_1=w_1λ/4πT_c \
v_2=w_2λ/4πT_c
$$
4.3 速度分辨率
离散傅里叶变换的理论指出,两个离散频率 $w_1$ 和 $w_2$ 在 $Δw = w_2 – w1 > 2π / N$ 个弧度/样本时,是可以分辨的。
由于 $Δw$ 是由 $Δφ=4πvT_c/λ$定义的,因而当帧周期为 $Tf = NT_c$ 时,可通过数学方法推导出速度分辨率:
$$
v>v_{res}=λ/2T_f
$$
可知,雷达的速度分辨率与帧时间 $T_f$ 成反比
5 角度测量
5.1 角度测量条件
FMCW 雷达系统可以使用水平面估算反射信号的角度,该角度也称为到达角 (AoA),如下图所示:
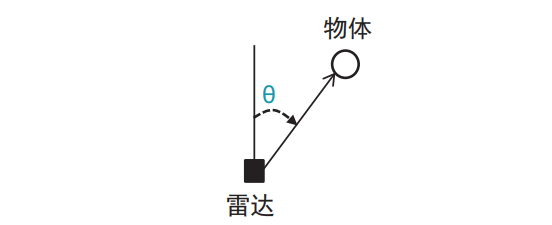
需要注意的是雷达估算角度至少需要两个 Rx 天线,如下图所示:
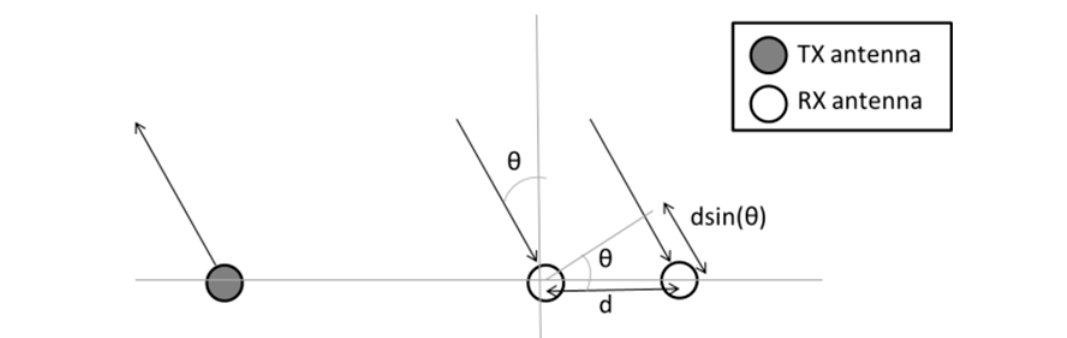
5.2 角度测量推导
我们知道,对于同一个物体,两个接受天线接受的相位差为:
$$
Δφ=wΔt
$$
其中,$w=2πf_c$, $Δt=dsin(θ)/c$
因此:
$$
Δφ=2πf_cdsin(θ)/c \
= 2πdsin(θ)/λ
$$
因此,角度可以通反三角函数得到:
$$
θ = sin^{-1}(Δφλ/2πd)
$$
注意,$Δφ$ 取决于 $sin(θ)$,这被称为非线性依赖关系。
$sin(θ)$仅在$θ$的值很小时,才是线性函数的近似值: $sin(θ)=θ$。因此,估算准确度取决于 AoA,且在 $θ$ 的值很小时更准确,如下图所示: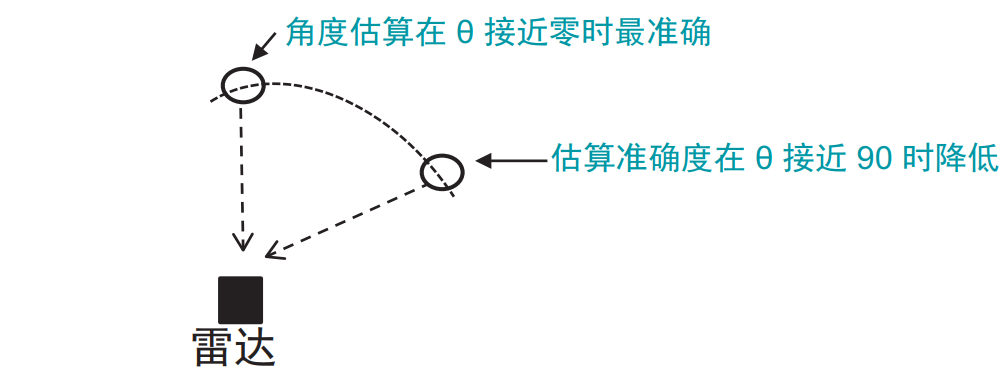
与速度获取计算方式相似,想计算物体的角度偏差,需要计算不同接受天线之间的相位差,好了第三个角度 FFT 来了,还是参考图像如下:

5.3 最大视场角
雷达的最大角视场由雷达可以估算的最大 AoA 来界定,如下: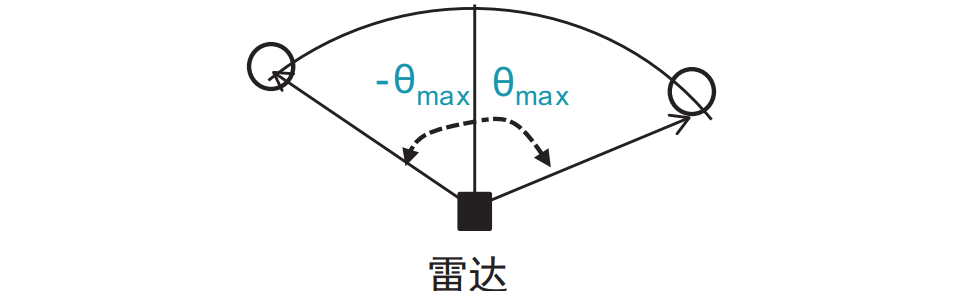
由于角度的精准测量受制于 $|Δw| < 180°$,对应关系有
$$
2πdsin(θ)/λ < π
$$
因此,角度最大为:
$$
θ_{max} = sin^{-1}(λ/2d)
$$
可知:两个天线之间的间隔 $d = λ/2$ 会导致 ±90°的最大角视场
6. 总结与效果
不同频率的雷达测量距离不同、最大探测角度也不同。目前Radar最基础的算法就是FFT,基于距离FFT、速度FFT以及角度FFT获取物体的运动信息,最终得到雷达图像。
Radar的典型效果如下所示:
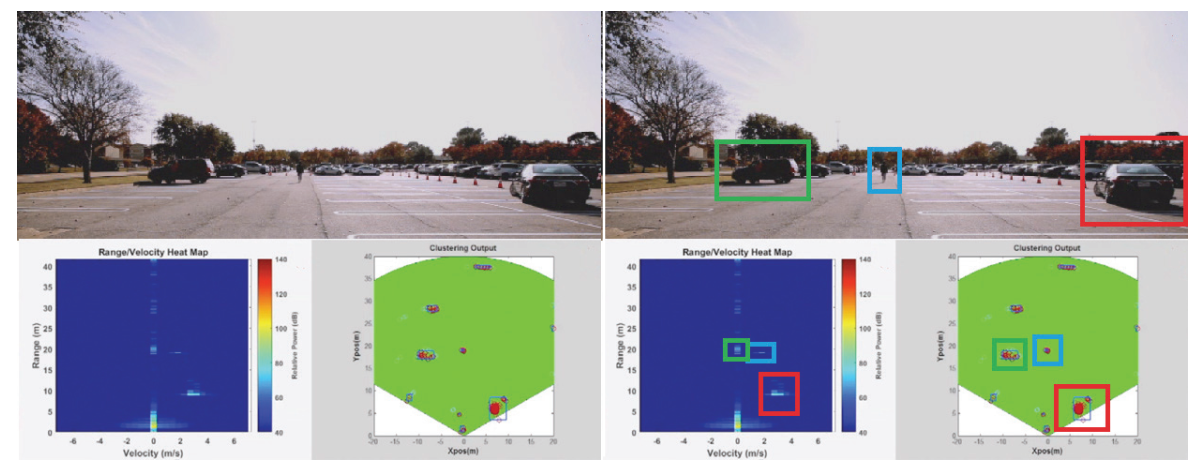
可以看出,目前3D Radar探测效果为一个平面数据,只有速度v、距离d以及角度θ信息,缺少了高度h信息,而这个在后续的4D Radar中进行了优化,这个我们后面再讲。
参考文献
[1] 毫米波雷达传感器基础知识
[2] MIMO Radar
如果您对ADAS感兴趣,欢迎关注我的公众号、知乎、CSDN等,同时发表文章中使用源码会在我的GitHub进行开源(网页About Me中有公众号、Github等信息)